Примечание

ЭТО АРХИВНАЯ ВЕРСИЯ КУРСА!

Материалы предназначаются для пересдающих дисциплину "ОП.04 - Основы алгоритмизации и программирования" в соответствии с учебными планами СПО годов набора ДО 2023-го.

Материалы были перенесены со старого сайта с минимальной доработкой, поэтому не все возможности курса могут работать как ожидается, где-то может слететь форматирование.

Домашние задания в рамках курса проверяться не будут!

ОП.04 - 15 - Итерация и итеративный процесс. Случайность в программировании. Проблемы точности вычислений

Код примера для практической работы

Итерация и итеративный процесс

Технология итерационной разработки характеризует жизненный цикл проекта программного обеспечения, включающий несколько итераций. Итерация состоит из примерно последовательного набора задач, выбранных из всех без исключения разделов разработки программного обеспечения. Часто такой подход называют итеративным подходом.

Итеративный подход (англ. iteration - «повторение») в разработке программного обеспечения — это выполнение работ с непрерывным анализом полученных результатов и корректировкой последующих этапов работы. Проект при этом подходе в каждой фазе развития проходит повторяющийся цикл: Планирование — Реализация — Проверка — Корректировка (англ. plan-do-check-act cycle / PDCA).

PDCA | block

PDCA (англ. «Plan-Do-Check-Act» — планирование-действие-проверка-корректировка) — методология принятия решения, используемая в управлении качеством.Также известен как цикл Деминга, цикл Шухарта, принцип Деминга-Шухарта (Деминг говорил PDSA (Plan-Do-Study-Act); Шухарт — Plan-Do-Check-Act).

Уильям Эдвардс Деминг | sm
Уильям Эдвардс Деминг

Деминг, Уильям Эдвардс; Эдвард Деминг (англ. William Edwards Deming, 14 октября 1900 — 20 декабря 1993) — американский учёный, статистик и консультант по менеджменту. Наибольшую известность Деминг приобрел, благодаря доработанному им циклу Шухарта, который теперь весь мир называет циклом Шухарта — Деминга (PDCA).

Уолтер Эндрю Шухарт | sm
Уолтер Эндрю Шухарт

Уолтер Эндрю Шухарт (англ. Walter Andrew Shewhart; 18 марта 1891 — 11 марта 1967) — американский учёный и консультант по теории управления качеством.

Методология PDCA представляет собой алгоритм действий руководителя по управлению процессом и достижению его целей и состоит из:

планирования — установления целей и процессов, необходимых для достижения целей, планирования работ по достижению целей процесса и удовлетворения потребителя, планирования выделения и распределения необходимых ресурсов;
выполнения — выполнение запланированных работ;
проверки — сбора информации и контроль результата на основе ключевых показателей эффективности (KPI), получившегося в ходе выполнения процесса, выявления и анализа отклонений, установления причин отклонений;
воздействия (управления, корректировки) — принятия мер по устранению причин отклонений от запланированного результата, изменений в планировании и распределении ресурсов.

В практической деятельности цикл PDCA применяется многократно с различной периодичностью. При выполнении основной деятельности цикл PDCA применяется с периодичностью циклов отчетности и планирования. При выполнении корректирующих действий длительность PDCA может быть меньше или больше длительности циклов отчетности и планирования и устанавливается в зависимости от характера, объема, длительности и содержания мероприятий по устранению причин отклонения.

Что такое итерационная разработка?

Итеративный процесс (также итеративный подход или итерационная разработка) в программировании — это подход при котором разработка программного продукта делится на четкие определенные шаги, называемые итерациями. Конкретный набор шагов зависит от проекта и используемой методологии разработки.

Проект, в котором применяется итерационная разработка, имеет жизненный цикл, состоящий из нескольких итераций. Итерация включает приблизительно последовательный набор задач бизнес-моделирования, требований, анализа и проектирования, реализации, тестирования и развертывания в различных пропорциях, в зависимости от расположения итерации в цикле разработки. Итерации на начальном этапе и этапе уточнения фокусируются на управлении, требованиях и проектировании; итерации на этапе построения фокусируются на проектировании, реализации и тестировании; а итерации на этапе внедрения фокусируются на тестировании и развертывании.

Преимущества итеративного подхода в разработке:

снижение воздействия серьёзных рисков на ранних стадиях проекта, что ведет к минимизации затрат на их устранение;
организация эффективной обратной связи проектной команды с потребителем (а также заказчиками, стейкхолдерами) и создание продукта, реально отвечающего его потребностям;
акцент усилий на наиболее важные и критичные направления проекта;
непрерывное итеративное тестирование, позволяющее оценить успешность всего проекта в целом;
раннее обнаружение конфликтов между требованиями, моделями и реализацией проекта;
более равномерная загрузка участников проекта;
эффективное использование накопленного опыта;
реальная оценка текущего состояния проекта и, как следствие, большая уверенность заказчиков и непосредственных участников в его успешном завершении;
затраты распределяются по всему проекту, а не группируются в его конце.

В начальном проекте по отношению к его ключевым требованиям с большой вероятностью будут содержаться ошибки. Позднее обнаружение дефектов проекта приводит к дорогостоящим затратам и, в некоторых случаях, даже к прекращению проекта. Любой проект влечет за собой определенные риски. Чем раньше в жизненном цикле можно проверить отсутствие рисков, тем более точно можно выполнять планирование. Многие риски не удается обнаружить до тех пор, пока не будет предпринята попытка интеграции системы. Невозможно предугадать все риски, независимо от опыта коллектива разработчиков.

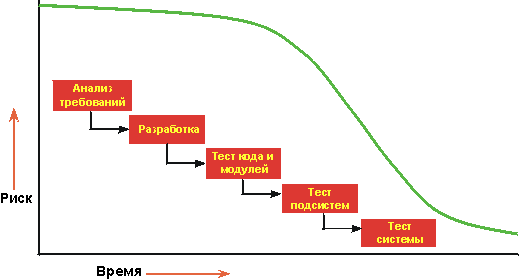
Пять шагов итеративного процесса

Итеративный процесс может быть полезен на протяжении всего жизненного цикла проекта. В итеративном процессе ваши цели и требования принимаются в качестве отправной точки проекта. После этого команда будет производить тестирование, разработку прототипов и итерацию для достижения максимально эффективного результата. Для этого необходимо соблюдать нижеследующие правила.

Составление плана и требований

На этом шаге итеративного процесса определяется план проекта, а также выполняется согласование с общими целями проекта. Именно в этой точке проекта формулируются все самые значительные требования, от выполнения которых зависит успешность реализации проекта. Без этого действия итерация может не достичь своей цели.

Анализ и проектирование

На этом шаге вы с вашей командой занимаетесь бизнес-потребностями и техническими требованиями своего проекта. Если на первом шаге определялись цели, то на втором вы продумываете проект, который в конечном счёте поможет достичь этих целей.

Реализация

На третьем шаге создаётся первая итерация реализации проекта. Данная итерация основывается на результатах анализа и проектирования и помогает достичь конечной цели проекта. Уровень детализации и время, затрачиваемое на эту итерацию, зависит от проекта.

Тестирование

После получения первой итерации производится её тестирование наиболее подходящим способом.

Рассмотрение и оценка результата

После тестирования производится оценка успешности итерации и согласование необходимых изменений. Достигает ли эта итерация цели проекта? Почему? Если требуются изменения, можно возобновить итеративный процесс и начать со второго шага, создав следующую итерацию. Помните, что первоначальный план и цели должны быть одинаковыми для всех итераций. Продолжайте работу на основе предыдущей итерации, пока не добьётесь желаемого результата.

Итеративный процесс может длиться неделями или месяцами в зависимости от количества итераций, через которые вам приходится пройти. Если всякий раз при повторном запуске итеративного процесса итерация будет сосредоточена на целях проекта, вы сможете всегда держать свои ориентиры в поле зрения.

Случайность в программировании

В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью. Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.

Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность.

Часто требуется не просто одно число, а несколько случайных чисел, генерируемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем (от англ. seed). Один из наиболее популярных подходов заключается в том, чтобы применить какую-то сложную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.

Функция искажения будет принимать одно значение, а возвращать другое. Назовём её rnd().

rnd(Input) -> Output

Начнём с того, что rnd() - это простая функция, которая всего лишь прибавляет единицу.

rnd(x) = x + 1

Если значение нашего семени 1, то rnd() создаст ряд 1, 2, 3, 4... Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь rnd() добавляет константу вместо 1.

rnd(x) = x + c

Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22... Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало - круг из чисел!

Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.

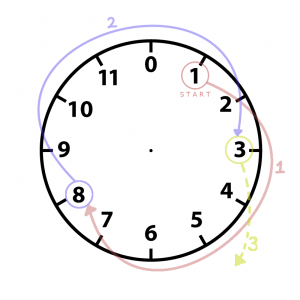
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать. Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.

Теперь давайте переделаем функцию rnd() так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.

rnd(x) = (x + c) % m

На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9... что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.

Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.

До сих пор мы делали "прыжки" за счёт добавления, но что если использовать умножение? Умножим х на константу a.

rnd(x) = (ax + c) % m

Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:

(а - 1) должно делиться на все простые множители m
(а - 1) должно делиться на 4, если m делится на 4

Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.

Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.

Еще один способ - это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее случайное число, как в программе с бросанием кубика.

Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:

x(n) = (a * x(n - 1) + c) % m

Где начальное значение х - это семя, а - множитель, с - константа, m - оператор остатка от деления.

То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро. В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания.

В JavaScript встроен объект Math, который содержит различные математические функции и константы. И функция для генерации псевдослучайных чисел в нем уже реализована посредством Math.random(), которая в качестве семени использует значение таймштампа с точностью до миллисекунды на момент вызова. При вызове Math.random() возвращает псевдослучайное число в диапазоне от 0 (включительно) до 1 (но не включая 1!).

Пример:


console.log( Math.random() ); // 0.1234567894322

В виде функции можно вызвать например так:

function getRandom() {
  return Math.random();
}

Следующий пример возвращает случайное число в заданном интервале. Возвращаемое значение не менее (и может быть равно) min и не более (и не равно) max.

function getRandomArbitrary(min, max) {
  return Math.random() * (max - min) + min;
}

А вот этот пример возвращает случайное целое число в заданном интервале. Возвращаемое значение не менее min (или следующее целое число, которое больше min, если min не целое) и не более (но не равно) max.

function getRandomInt(min, max) {
  min = Math.ceil(min);
  max = Math.floor(max);
  return Math.floor(Math.random() * (max - min)) + min; //Максимум не включается, минимум включается
}

[!INFO]
Одна из часто используемых операций при работе с числами — это округление. В JavaScript есть несколько встроенных функций для работы с округлением:
Math.floor() - Округление в меньшую сторону: 3.1 становится 3, а -1.1 — -2.
Math.ceil() - Округление в большую сторону: 3.1 становится 4, а -1.1 — -1.
Math.round() - Округление до ближайшего целого: 3.1 становится 3, 3.6 — 4, а -1.1 — -1.
Может показаться заманчивым использовать Math.round() для округления, но это может сделать распределение неравномерным, что может оказаться неприемлемым для ваших нужд.

Функция getRandomInt() выше включает минимальное значение, но не включает максимальное. Но что если вам нужно, чтобы включалось и минимальное, и максимальное значение? Функция getRandomIntInclusive() решает этот вопрос.

function getRandomIntInclusive(min, max) {
  min = Math.ceil(min);
  max = Math.floor(max);
  return Math.floor(Math.random() * (max - min + 1)) + min; //Максимум и минимум включаются
}

Проблемы точности вычислений

Существует множество ситуаций, в которых точность округления и точность в вычислениях с плавающей точкой (запятой в стандартах записи чисел в РФ) могут работать для создания неожиданных для программиста результатов.

Прежде чем продолжить, давайте разберемся с одной маленькой концепцией: как числа представлены в вычислительных целях? Очень маленькие и очень большие числа обычно хранятся в экспоненциальном представлении. Они представлены как:

\text{число} \times \text{основание}^\text{экспонента}

Кроме того, число нормализуется, если оно записано в экспоненциальном представлении с одной ненулевой десятичной цифрой перед десятичной точкой. Например, число 0,0005606 в экспоненциальном представлении и нормализованное будет представлено как:

5,606 \times 10^{-4}

В информатике принято использовать формулу экспоненциальной записи числа:

N = M \times n^p

где:

$N$ — записываемое число;
$M$ — мантисса;
$n$ — основание показательной функции;
$p$ (целое) — порядок;
$n^{p}$ — характеристика числа.

$M$ — это количество значащих цифр, которые не включают нулей, а основание представляет собой используемую базовую систему, которая здесь десятичная (10). Экспонента представляет собой количество мест, на которое необходимо переместить точку счисления влево или вправо для правильного представления.

Есть два способа отображения чисел в арифметике с плавающей запятой: одинарная точность и двойная точность. Одинарная точность использует 32 бита, а двойная точность использует 64 бита для арифметики с плавающей запятой. В отличие от многих других языков программирования, JavaScript не определяет различные типы числовых типов данных и всегда хранит числа как числа с плавающей запятой двойной точности в соответствии с международным стандартом IEEE-754.

Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 для хранения положения десятичной точки и 1 бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

console.log( 1e500 ); // Infinity

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript — это потеря точности.

Посмотрите на это (неверное!) сравнение:

console.log( 0.1 + 0.2 == 0.3 ); // false

Да-да, сумма 0.1 и 0.2 не равна 0.3.

Странно! Что тогда, если не 0.3?

console.log( 0.1 + 0.2 ); // 0.30000000000000004

Ой! Здесь гораздо больше последствий, чем просто некорректное сравнение. Представьте, вы делаете интернет-магазин и посетители формируют заказ из 2-х позиций за $0.10 и $0.20. Итоговый заказ будет $0.30000000000000004. Это будет сюрпризом для всех.

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит — единиц и нулей. Но дроби, такие как 0.1, 0.2, которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое 0.1? Это единица делённая на десять — 1/10, одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: 1/3, которая становится бесконечной дробью 0.33333(3).

Деление на 10 гарантированно хорошо работает в десятичной системе, но деление на 3 — нет. По той же причине и в двоичной системе счисления, деление на 2 обязательно сработает, а 1/10 становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

console.log( 0.1.toFixed(20) ); // 0.10000000000000000555

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему 0.1 + 0.2 — это не совсем 0.3.

[!INFO]
Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

let sum = 0.1 + 0.2;
console.log( sum.toFixed(2) ); // 0.30

Помните, что метод toFixed всегда возвращает строку. Это гарантирует, что результат будет с заданным количеством цифр в десятичной части. Также это удобно для форматирования цен в интернет-магазине $0.30. В других случаях можно использовать унарный оператор +, чтобы преобразовать строку в число:

let sum = 0.1 + 0.2;
console.log( +sum.toFixed(2) ); // 0.3

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она всё равно появляется при финальном делении:

console.log( (0.1 * 10 + 0.2 * 10) / 10 ); // 0.3
console.log( (0.28 * 100 + 0.14 * 100) / 100); // 0.4200000000000001

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Иногда можно попробовать полностью отказаться от дробей. Например, если мы в нашем интернет-магазине начнём использовать центы вместо долларов. Но что будет, если мы применим скидку 30%? На практике у нас не получится полностью избавиться от дроби. Просто используйте округление, чтобы отрезать «хвосты», когда надо.

Забавный пример

Попробуйте выполнить его:

// Привет! Я — число, растущее само по себе!
console.log( 9999999999999999 ); // покажет 10000000000000000

Причина та же — потеря точности. Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

[!INFO]
Другим забавным следствием внутреннего представления чисел является наличие двух нулей: 0 и -0. Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль. В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.